8.1. Siły międzycząsteczkowe w cieczach

Obecnie rozważymy oddziaływania wzajemne cząsteczek w gazach, cieczach i ciałach stałych. Zachowanie się gazów rzeczywistych różni się wyraźnie od zachowania się gazu doskonałego w przypadkach różnych od warunków normalnych, szczególnie przy dużym ciśnieniu. Należy uwzględnić zatem, że cząsteczki mają skończone rozmiary i nie są punktami materialnymi oraz że istnieją oddziaływania wzajemne cząsteczek będących w odległościach większych od odległości wynikającej z ich wzajemnego kontaktu podczas zderzenia.

Rozważmy siły oddziaływania międzycząsteczkowego. Już bardzo prosta obserwacja ciał prowadzi do wniosku, że cząsteczki oddziałują na siebie siłami przyciągania i siłami odpychania. Jeżeli staramy się rozciągnąć jakieś ciało stałe, to natychmiast wystąpi siła reakcji, której pochodzenie tłumaczymy sumowaniem się sił przyciągania cząsteczek tego ciała. Podobna, lecz przeciwna reakcja występuje przy ściskaniu, gdy staramy się zmniejszyć odległości międzycząsteczkowe. Wnioskujemy stąd o istnieniu sił odpychania między cząsteczkami. Siły te rosną bardzo szybko w miarę zmniejszania się odległości między cząsteczkami. Na il. 8.2a przedstawione są krzywe zależności tych sił od odległości $r$ między cząsteczkami. Wypadkowa krzywa ma wyraźne minimum i przecina oś $r$ w odległości $r_{0}$ , przy której cząsteczki znajdują się w równowadze.

Zależność a) sił oddziaływania molekularnego, b) energii potencjalnej od odległości międzycząsteczkowej — Ilustracja 8.2. **Zależność: a) sił oddziaływania molekularnego, b) energii potencjalnej od odległości międzycząsteczkowej**

Na il. 8.2b przedstawiona jest krzywa zależności energii potencjalnej oddziałujących na siebie cząsteczek od odległości między nimi. Pozwala ona na wyciągnięcie kilku ważnych wniosków. Zauważmy, że „głębokość” minimum krzywej $U_{min}$ informuje nas o tym, jak silnie cząsteczki są związane ze sobą, jeżeli znajdują się w odległości równowagi $r_{0}$ ; $U_{min}$ oznacza wtedy energię, jaką należałoby dostarczyć, aby oddalić cząsteczki poza zasięg ich oddziaływania (tzn. na odległość $r$ , gdzie siły ich wzajemnego oddziaływania dążą do zera i wynikająca stąd energia potencjalna praktycznie się już nie zmienia). Ze względu na kształt krzywej $U(r)$ obszar ujemnych wartości $U$ bywa nazywany lejem energii potencjalnej, wewnątrz którego mogą być uwięzione cząsteczki.

Cząsteczki w ciele stałym wykonują drgania o energii całkowitej wynikającej z zasady ekwipartycji energii (patrz rozdział 7.D1. Dodatek: Energia wewnętrzna gazu – zasada ekwipartycji energii (temat nadobowiązkowy)), która w tym przypadku przydziela każdej z drgających cząsteczek energię równą $k T$ $kT/2$ dla energii kinetycznej drgań plus $kT/2$ dla energii potencjalnej drgań). Zatem energia całkowita każdej z drgających cząsteczek wyniesie $E_{cz}=kT-U_{min}$ . Widzimy, że w przypadku, gdy $U_{min}>kT$ , energia całkowita cząsteczek będzie ujemna, $E_{cz} {mniejsze} 0$ , i drgania cząsteczek nie spowodują wyrwania ich z leja energii potencjalnej (il. 8.2b), czyli cząsteczki nie oddalą się od siebie poza zasięg ich wzajemnego oddziaływania. Wtedy utworzą one ciało stałe, w którym cząsteczki są utrzymane siłami wzajemnego oddziaływania w bliskiej odległości.

Natomiast gdy $U_{min}$ będzie małe w porównaniu z energią $k T$ , to termiczny ruch cząsteczek spowoduje zerwanie ich wzajemnych więzów i cząsteczki utworzą stan gazowy, bowiem całkowita energia cząsteczki będzie dodatnia $E_{cz}>0$ . Mówimy wtedy, że cząsteczka może wyrwać się z leja energii potencjalnej. Wtedy cząsteczki oddalą się poza zasięg wzajemnego oddziaływania. W przypadkach pośrednich, gdy $U_{min}\approx kT$ będziemy mieli do czynienia z fazą ciekłą. Zatem, znając wykres energii potencjalnej wynikającej z sił wzajemnego oddziaływania cząsteczek, możemy przewidzieć, czy w określonej temperaturze substancja złożona z dużej liczby cząsteczek znajdzie się w stanie stałym, ciekłym czy gazowym, według następującego kryterium:

U_{min}\{\begin{array}{c} \lt kT\,\,-\, gaz\\ \approx kT\,\,-\, ciecz\\ >kT\,\,-\, cia\mathchar'40\mkern-5mu l o\, sta\mathchar'40\mkern-5mu l e \end{array}

Na il. 8.2a zaznaczono odległość $R_{M}$ , powyżej której oddziaływanie jest tak słabe, że możemy z dobrym przybliżeniem założyć całkowity brak oddziaływania. Wprowadzenie odległości $R_{M}$ , która nosi nazwę promienia działania molekularnego, pozwala na znaczne uproszczenie rozumowania, chociaż zdajemy sobie sprawę, że $R_{M}$ nie ma dokładnie określonej wartości. Rozpatrzenie krzywych oddziaływania międzycząsteczkowego prowadzi do wniosku, że w odległości większej od ok. $10^{-9}$ cząsteczki praktycznie nie oddziałują na siebie, czyli $R_{M} {mniejsze} 10^{-9}\, m$ (jeżeli porównamy tę odległość z rozmiarami typowej cząsteczki, to dojdziemy do wniosku, że promień działania molekularnego jest od ok. 5 do 10 razy większy od wymiaru cząsteczki).

Napięcie powierzchniowe

Zapytajmy teraz, jak wprowadzenie sił oddziaływania międzycząsteczkowego wpłynie na stan gazu czy cieczy. Na il. 8.3 przedstawiono trzy różne sytuacje z udziałem cząsteczek znajdujących się w gazie wewnątrz naczynia. Cząsteczka oznaczona „1” znajduje się w głębi naczynia. Cząsteczki znajdujące się wewnątrz obszaru kulistego o promieniu $R_{M}$ otaczającego tę cząsteczkę będą ją przyciągały lub odpychały ze wszystkich stron. To oddziaływanie – uśrednione w czasie – daje w efekcie wypadkową siłę działającą na cząsteczkę „1” równą zero. Jednym jego skutkiem jest chaotyczne przemieszczenie tej cząsteczki we wnętrzu cieczy lub gazu. Podobnemu oddziaływaniu będą poddane cząsteczki w sytuacji takiej, jak sytuacja cząsteczki „2”, których sfery działania molekularnego znajdują się tuż pod powierzchnią cieczy. Zatem na zachowanie cząsteczek będących w sytuacji cząsteczek „1” i „2” siły oddziaływania międzycząsteczkowego nie mają żadnego wpływu.

Ilustracja 8.3. **Sytuacja różnych cząsteczek wewnątrz płynu i w pobliżu ścianki naczynia $P-P'$**

Inaczej sprawa przedstawia się dla cząsteczki „3”, której sfera działania molekularnego wystaje poza powierzchnię swobodną cieczy $P-P'$ . Podziała na nią siła wypadkowa wynikająca z oddziaływania z cząsteczkami otoczenia, która będzie skierowana w głąb cieczy. W takiej sytuacji znajdą się wszystkie cząsteczki zlokalizowane w warstwie przypowierzchniowej o grubości równej $R_{M}$ . Na il. 8.4 przedstawiono taką cząsteczkę. Sferę działania molekularnego podzielono płaszczyznami równoległymi do powierzchni cieczy na cztery obszary: $a$ , $b$ , $c$ i $d$ w ten sposób, że obszary $a$ i $d$ są równe sobie; podobnie obszary $b$ i $c$ są równe sobie. Siły wypadkowe od cząsteczek z obszarów $b$ i $c$ wzajemnie się kompensują. Obszar $a$ nie jest zajęty przez cząsteczki gazu i nie kompensuje działania pochodzącego z obszaru $d$ . Zatem na cząsteczkę w środku sfery będzie działać siła wypadkowa $F_{i}$ pochodząca od cząsteczek znajdujących się w obszarze $d$ . Siła ta jest proporcjonalna do liczby cząsteczek $N'$ znajdujących się w tym obszarze. Całkowita siła działająca na wszystkie cząsteczki znajdujące się w warstwie przypowierzchniowej wyraża się sumą:

F'=F_{1}+F_{2}+...=\overset{N'}{\underset{i=1}{\sum}}F_{i}

gdzie $N'$ – liczba cząsteczek w warstwie przypowierzchniowej o grubości $R_{M}$ .

Zatem $N'=n_{c}R_{M}S$ , gdzie $n_{c}$ – koncentracja cząsteczek, czyli liczba cząsteczek w jednostce objętości, $S$ – powierzchnia ścianki naczynia.

Jeżeli przez $\overline{F_{i}}$ oznaczymy wartość średnią sił działających na cząsteczki w warstwie przypowierzchniowej, to dodatkowa siła działająca na płyn (gaz lub ciecz) i pochodząca od wszystkich $N'$ cząsteczek wyniesie:

F=N'\overline{F_{i}}=n_{c}R_{M}S\overline{F_{i}}

lub

F=K_{\sigma}S

gdzie stały czynnik $K_{\sigma}=n_{c}R_{M}\overline{F_{i}}$ .

Dzieląc siłę $F$ przez pole powierzchni $S$ , otrzymujemy dodatkowe ciśnienie $p_{d}$ działające na płyn na skutek sił wzajemnego przyciągania cząsteczek:

p_{d}=K_{\sigma}

( 8.1 )

Jest ono ściśle związane z tzw. napięciem powierzchniowym działającym w cieczy, którego definicję podajemy niżej.

Cząsteczki w warstwie powierzchniowej cieczy mają wyższą energię niż cząsteczki wewnątrz cieczy. Ponieważ cząsteczki wewnątrz cieczy znajdują się blisko siebie, siły wzajemnego przyciągania cząsteczek działają we wszystkich kierunkach, dając siłę wypadkową równą zeru. Natomiast cząsteczki w warstwie powierzchniowej są w innej sytuacji. Na te cząsteczki pozostała część cieczy wywiera siłę przyciągania skierowaną w głąb cieczy (il. 8.3). Dlatego warstwa powierzchniowa cieczy wywołuje ciśnienie w jej wnętrzu. Ciśnienie to, niezależne od ciśnienia atmosferycznego, bywa całkiem spore. Przykładowo, dla kropli wody o średnicy 1 µm przekracza ono jedną atmosferę. Z kolei ścianki naczynia, w którym zamknięta jest ciecz, nie odczuwają oddziaływania warstwy powierzchniowej.

Widzimy więc, że cząsteczki w warstwie powierzchniowej będą miały oprócz energii kinetycznej ruchu cieplnego jeszcze energię potencjalną związaną z istnieniem sił oddziaływania międzycząsteczkowego. Natomiast cząsteczki w głębi cieczy mają tylko energię kinetyczną. Cząsteczki, które chcą przejść z głębi cieczy na powierzchnię, muszą wykonać pracę przeciwko siłom przyciągania pochodzącym od innych cząsteczek cieczy. Zatem cząsteczki w warstwie powierzchniowej będą miały tyle energii potencjalnej, w stosunku do cząsteczek w głębi cieczy, ile wymaga to pracy, aby się znalazły w tej warstwie.

W stanie równowagi układ ciał zawsze dąży do tego, aby miał możliwie najniższą energię, dlatego każda ciecz dąży do zminimalizowania swojej powierzchni. Ponieważ ciecz jest nieściśliwa, więc zmniejszenie powierzchni cieczy nie może się odbyć przez zmniejszenie jej objętości, ale przez takie dopasowanie kształtu, aby stosunek powierzchni do objętości był najmniejszy. Z geometrii wiadomo, że taki warunek spełnia ciało w kształcie kuli. Dlatego krople cieczy zawieszone w powietrzu i innych ośrodkach przybierają kształt kulisty.

a) Siły powierzchniowe pochodzące od błonki górnej równoważą siły powierzchniowe od błonki dolnej, b) po zerwaniu błonki dolnej siły powierzchniowe od błonki górnej są równoważone przez siłę zewnętrzną — Ilustracja 8.5. a) siły powierzchniowe pochodzące od błonki górnej równoważą siły powierzchniowe od błonki dolnej, b) po zerwaniu błonki dolnej siły powierzchniowe od błonki górnej są równoważone przez siłę zewnętrzną $F$

Ciecz dąży do zmniejszania wymiarów powierzchni swobodnej, ponieważ warstwa powierzchniowa działa podobnie do naciągniętej błonki sprężystej, w której działają siły napięcia. W celu zilustrowania tego stanu wykonajmy następujące doświadczenie. Ramkę drucianą $A B C D$ z poprzeczką $P P'$ przedstawioną na il. 8.5 zanurzamy w wodzie z rozpuszczonym mydłem. Po wyjęciu z wody na ramce utworzy się błonka. W przypadku a) siły działające na poprzeczkę od strony obu części błonki – górnej i dolnej równoważą się wzajemnie i poprzeczka jest w spoczynku. Po rozerwaniu dolnej błonki w przypadku b) poprzeczka zaczyna przesuwać się w górę i należy przyłożyć siłę $F$ , przez zawieszenie np. na niej ciężarka, do zrównoważenia sił pochodzących od górnej błonki. Doświadczalnie stwierdzono, że siła równoważąca $F$ jest proporcjonalna do długości krawędzi $l$ :

F=2\sigma l

( 8.2 )

Współczynnik proporcjonalności $\sigma$ nosi nazwę napięcia powierzchniowego. Czynnik $2$ we wzorze wynika stąd, że na poprzeczkę działają siły pochodzące od dwóch warstw powierzchniowych cieczy rozpiętej w postaci błonki mydlanej, z których każda działa siłą:

F_{\sigma}=\sigma l

( 8.3 )

Więc napięcie powierzchniowe możemy zdefiniować jako stosunek wartości siły, jaką warstwa powierzchniowa cieczy działa na ograniczającą ją krawędź, do długości tej krawędzi.

Z wzoru (8.2) wynika, że jednostką napięcia powierzchniowego jest niuton dzielony przez metr, $N/m$ . Wartość napięcia powierzchniowego zależy od rodzaju cieczy, otaczającego środowiska i jej temperatury. Na przykład, dla wody w ośrodku powietrznym w temperaturze $20^{\circ}C$ : $\sigma=72,7\cdot10^{3}N/m$ , zaś w temperaturze $100^{\circ}C$ : $\sigma=58,8\cdot10^{3}N/m$ .

Menisk i zjawisko włoskowatości

Łatwo można zauważyć, przyglądając się poziomowi cieczy na granicy ze ścianką naczynia, że ciecz w tym miejscu jest albo nieco podniesiona do góry, albo obniżona w dół (il. 8.6); jest to tzw. menisk. W pierwszym przypadku jest to tzw. menisk wklęsły, a w drugim – menisk wypukły. Menisk można scharakteryzować za pomocą kąta granicznego $\vartheta$ między ścianką naczynia i styczną do powierzchni menisku w miejscu jego zetknięcia ze ścianką (patrz il. 8.6). Kąt ten nosi również nazwę kąta zwilżania. Gdy kąt zwilżania jest mniejszy od $90^{\circ}$ , to mówimy, że ciecz zwilża ściankę naczynia, natomiast gdy jest on większy od $90^{\circ}$ , to mówimy, że ciecz nie zwilża ścianki.

Ilustracja 8.6. **Menisk: a) wklęsły, b) wypukły; kąt graniczny $\vartheta$**

Menisk występuje dlatego, że cząsteczki cieczy znajdujące się w pobliżu ścianki naczynia oddziałują nie tylko ze sobą, ale również z cząsteczkami ścianki. Rozważmy przykład cząsteczki $A$ , znajdującą się w pobliżu ścianki naczynia, jak na il. 8.7a. Obszar jej oddziaływania z innymi cząsteczkami zawarty jest w objętości kuli o promieniu działania molekularnego. W obszarze tym znajdują się cząsteczki cieczy, jak również cząsteczki ścianki naczynia.

Wypadkowa sił przyciągania cząsteczek cieczy $\vec{F_{1}}$ jest skierowana pod kątem w głąb cieczy, natomiast wypadkowa $\vec{F_{2}}$ pochodząca od cząsteczek ścianki jest skierowana prostopadle do ścianki. Kierunek wypadkowej siły $\vec{F}=\vec{F_{1}}+\vec{F_{2}}$ zależy od tego, jak duża jest siła $\vec{F_{2}}$ (o tym decydują cząsteczki, z jakich zbudowana jest ścianka) w porównaniu z siłą $\vec{F_{1}}$ . Otóż o kształcie menisku decyduje kierunek wypadkowej $\vec{F}$ tych dwóch sił, dlatego że powierzchnia cieczy ustawia się zawsze prostopadle do wypadkowej siły działającej na cząsteczki na powierzchni cieczy.

Ilustracja 8.7. **Sytuacja cząsteczki $A$ w pobliżu ścianki naczynia**

a) zasięg działania molekularnego, b) duża siła $F_{2}$ – menisk wklęsły, zwilżanie, c) menisk płaski, d) mała siła $F_{2}$ – menisk wypukły, brak zwilżania

Na il. 8.7 zaznaczono trzy przypadki:

wypadkowa siła $\vec{F}$ jest skierowana w stronę ścianki – otrzymujemy menisk wklęsły (il. 8.7b), to znaczy, że ciecz zwilża ściankę,
wypadkowa siła $\vec{F}$ jest skierowana równolegle do ścianki (siła $\vec{F_{1}}$ jest skierowana pod kątem do ścianki) – wynikiem jest menisk płaski (il. 8.7c),
wypadkowa siła $\vec{F}$ jest skierowana w głąb cieczy (il. 8.7d) – menisk jest wypukły; ciecz nie zwilża ścianki.

Obliczymy teraz ciśnienie, jakie wywiera warstwa powierzchniowa na ciecz w cienkiej rurce o przekroju kołowym o promieniu $r$ (il. 8.8). W przypadku, gdy promień $r$ jest bardzo mały, można przyjąć, że powierzchnia cieczy ma kształt wycinka kuli. Na każdy mały element obwodu kolistego $\Delta l$ w miejscu styku powierzchni cieczy ze ścianką rurki działa siła $\Delta F$ styczna do powierzchni cieczy. Siłę tę rozłożymy na dwie składowe $\Delta F_{1}$ i $\Delta F_{2}=\Delta F\cos\alpha=-\sigma\Delta l\cos\vartheta$ (patrz il. 8.8). Uwzględniamy przy tym, że kąt $\alpha$ jest dopełnieniem kąta $\vartheta$ do $180^{\circ}$ (patrz il. 8.6). Zatem na cały obwód styku $2\pi r$ działa siła skierowana w głąb cieczy, równa $F_{2}=-\sigma2\pi r\cos\vartheta$ . Siła ta wywiera na ciecz dodatkowe ciśnienie, niezależnie od ciśnienia atmosferycznego. Aby otrzymać wartość tego dodatkowego ciśnienia, należy podzielić wartość siły $F_{2}$ przez pole powierzchni $S=\pi r^{2}$ :

p=-\frac{2\sigma\cos\vartheta}{r}

( 8.4 )

Znak minus w tym wzorze oznacza, że gdy kąt $\vartheta$ jest ostry, czyli gdy menisk jest wklęsły, to ciśnienie jest ujemne, i na odwrót, gdy kąt $\vartheta$ jest rozwarty – menisk wypukły – to ciśnienie jest dodatnie (bo cosinus jest ujemny dla kąta zawartego w przedziale od $90^{\circ}$ do $180^{\circ}$ ).

Ilustracja 8.8. **Składowa $\Delta F_{2}$ siły napięcia powierzchniowego powoduje ciśnienie dodatkowe działające na ciecz**

Obliczone przez nas ciśnienie dodatkowe przesuwa poziom równowagi cieczy w bardzo wąskich rurkach, których średnica wynosi około 1 mm lub mniej. Rurki takie noszą nazwę naczyń włoskowatych lub kapilarnych (od słowa łacińskiego capillus – włos). Jeżeli rurkę włoskowatą zanurzymy w cieczy, która ją zwilża, to na skutek ujemnego ciśnienia dodatkowego (wzór (8.4)) poziom cieczy wewnątrz rurki podniesie się ponad poziom cieczy w dużym naczyniu (il. 8.9a), i odwrotnie ciecz w naczyniu niezwilżanym się obniży (il. 8.9b).

Ilustracja 8.9. **Poziom cieczy w naczyniach włoskowatych: a) ciecz zwilżająca, b) brak zwilżania**

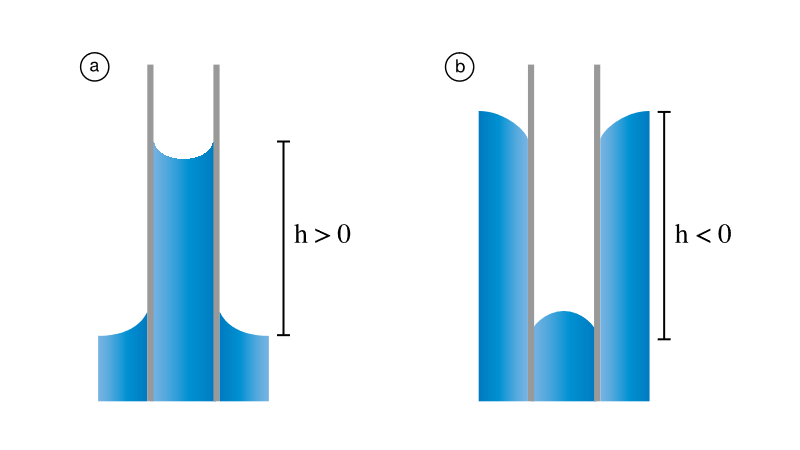
Możemy teraz łatwo obliczyć, na jaką wysokość $h$ podniesie się (lub opuści) ciecz w kapilarze. Warunek równowagi cieczy mówi, że suma ciśnienia hydrostatycznego $\varrho gh$ i ciśnienia dodatkowego $p=-\left(2\sigma\cos\vartheta\right)/r$ jest równa zeru: $\varrho gh-\left(2\sigma\cos\vartheta\right)/r=0$ . Stąd:

h=\frac{2\sigma\cos\vartheta}{\varrho gr}

( 8.5 )

Zjawisko włoskowatości jest często spotykane w życiu codziennym. Higroskopijność ciał, czyli zdolność do pochłaniania wilgoci, tłumaczymy zjawiskiem włoskowatości, którym charakteryzują się np. wata, tkaniny stosowane na ręczniki, papier, bibuła itp. Gleba również ma własności higroskopijne, ponieważ „rurki włoskowate” występujące w glebie podnoszą wodę aż do jej powierzchni, co zwiększa parowanie wody. Oczywiście nie należy sobie wyobrażać, że w glebie są jakieś „rurki” - chodzi tu o mikroskopijne pory, szczeliny, pęknięcia, itp., których średnice mogą dochodzić do 1 µm i mniej. W celu zatrzymania wilgoci, glebę orze się i bronuje, aby zniszczyć te „naczynia włoskowate”.

Pytania i problemy

Co rozumiesz przez sferę działania molekularnego?
Jak przedstawia się obraz działania sił międzycząsteczkowych w przypadku cząsteczki znajdującej się w warstwie powierzchniowej oraz cząsteczki w głębi cieczy?
Wyjaśnij, w jaki sposób powstaje napięcie powierzchniowe.
Co to jest menisk wklęsły i menisk wypukły?
Dlatego powierzchnia cieczy w pobliżu ścianki naczynia zagina się? Jaka jest sytuacja cząsteczki cieczy znajdującej się w pobliżu ścianki naczynia? Jak oddziałują cząsteczki cieczy z cząsteczkami ścianki?
Jaki sposób stosują rolnicy, aby zachować wilgoć w glebie w czasie suszy?