Wykonując to doświadczenie, przekonamy się, że wzór na drogę w ruchu jednostajnie przyspieszonym dobrze zgadza się z rzeczywistością. To znaczy, że wzór ten prawidłowo opisuje zależność drogi od czasu i wykresem tej zależności jest parabola. Wyznaczymy także wartość przyspieszenia kulki staczającej się po równi pochyłej.

Przy okazji poznamy ciekawy sposób przekształcenia krzywej na wykresie w linię prostą. Ułatwia to analizę niepewności pomiarowych oraz pozwala jasno unaocznić odchylenia pomiarów doświadczalnych od przewidywań teoretycznych.

Doświadczenie wykonujemy w następujący sposób:

Z zestawu do doświadczeń z mechaniki wybieramy dwa pręty o długości 1 m i łączymy je tak, aby utworzyły szyny, które ustawiamy na stole, podkładając na jednym końcu wsporniki. W ten sposób powstaje równia pochyła o niewielkim kącie nachylenia do poziomu (il. 1.52). Oznaczamy na niej kredą (lub w inny sposób) jednakowe odcinki drogi, na przykład co $l=10\text{cm}$.

Za pomocą stopera wykonujemy pomiary czasu staczania się kulki na coraz dłuższych odcinkach drogi. Mierzymy czas $t_1$ na drodze $s_1=l$, $t_2$ na drodze $s_2=2l$ itd. Kulkę puszczamy za każdym razem z wierzchołka równi. Każdy pomiar powtarzamy trzykrotnie, aby łącznie otrzymać trzy serie pomiarów.

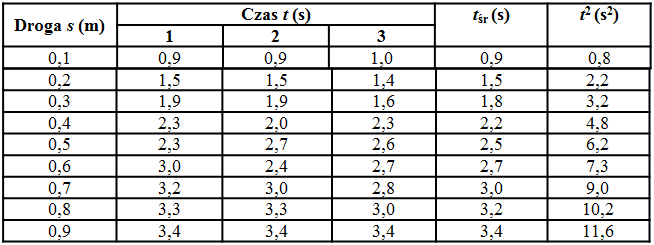
Dla każdej wartości drogi obliczamy średni czas ruchu kulki i wpisujemy go do rubryki $t_{\text{śr}}$ (tabela na il. 1.54). Dzięki wyznaczeniu wartości średniej uzyskujemy wyniki dokładniejsze niż w przypadku, gdybyśmy się ograniczyli do pojedynczego pomiaru (jak sądzisz – dlaczego?). Obliczamy wartości kwadratów czasów średnich i wpisujemy je w ostatniej rubryce tabelki.

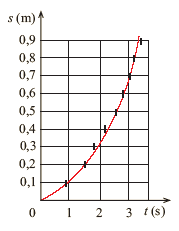
Sporządzamy wykres zależności drogi od czasu dla wartości uzyskanych podczas pomiaru. Na osi rzędnych odkładamy drogę $s$ w metrach, a na osi odciętych – czas w sekundach. Pamiętajmy o doborze właściwej skali na osiach, aby wykres był czytelny. Nanosimy punkty doświadczalne i wykreślamy krzywą, prowadząc ją „od ręki” między punktami doświadczalnymi (nie należy kreślić linii łamanej od punktu do punktu).

Sprawdzamy, czy otrzymana krzywa przypomina parabolę. Teoretyczny wzór na drogę w ruchu jednostajnie przyspieszonym (wzór (1.17 ) w rozdziale 1.4. Ruch jednostajnie przyspieszony) przedstawia, jak wiemy, funkcję kwadratową czasu:

Wykres zależności $s\text{(}t\text{)}$ bez wątpienia nie jest linią prostą. Zapisujemy wniosek, jaki wynika z krzywoliniowego charakteru $s\text{(}t\text{)}$.

Prześledzimy opracowanie wyników doświadczenia na przykładzie konkretnych danych otrzymanych w jednej ze szkół. Wyniki pomiarów i obliczeń podane są w tabeli na il. 1.54. Korzystając z nich, sporządzono wykres zależności $s$ od $t$, odkładając wartości $t_{\text{śr}}$ jako rzędne punktów doświadczalnych.

Wykreślona krzywa (il. 1.53) bardzo przypomina parabolę. Dzięki temu otrzymuje się potwierdzenie doświadczalne wzoru teoretycznego (1.44). Jeżeli otrzymaliśmy taki wynik, możemy się cieszyć, jednocześnie możemy odczuwać też pewien niedosyt, gdyż uzyskaliśmy tylko jakościowe potwierdzenie teorii.

Spróbujmy znaleźć potwierdzenie bardziej obiektywne i dokładniejsze. Gdybyśmy mieli do czynienia z funkcją liniową, a nie, jak w tym przypadku, z funkcją kwadratową, dużo łatwiej byłoby stwierdzić zgodność położenia punktów doświadczalnych z teoretyczną linią prostą (wystarczyłoby tylko przyłożyć linijkę). Spróbujmy zatem „wyprostować” parabolę odpowiadającą zależności drogi od czasu w ruchu jednostajnie przyspieszonym z zerową prędkością początkową.

Jeżeli na osi rzędnych będziemy odkładać drogę $s$, a na osi odciętych, zamiast wartości czasu $t$, wartości kwadratów czasu $t^2$, to powinniśmy otrzymać prostą. Wtedy w równaniu (1.45) jako zmienną niezależną traktujemy nie $t$, ale $t^2$, natomiast $s$ jako zmienną zależną. Otrzymujemy w ten sposób zależność liniową między $s$ a $t^2$:

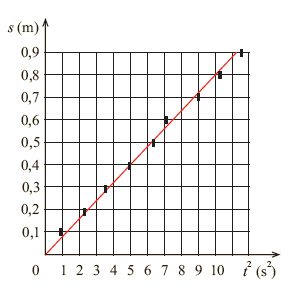
Wykorzystując ostatnią rubrykę w tabelce, możemy sporządzić wykres zależności $s$ od $t^2$. Wykres dla podanych wartości doświadczalnych przedstawiony jest na il. 1.55. Teraz widzimy wyraźnie, że punkty doświadczalne układają się wzdłuż prostej – nie mamy wątpliwości, że nasze doświadczenie potwierdza teoretyczny wzór na drogę jako funkcję czasu! Widzimy wprawdzie, że punkty pomiarowe nie leżą dokładnie na prostej, ale nie możemy oczekiwać czegoś takiego w doświadczeniu, którego wyniki są zawsze obarczone określoną niepewnością pomiarową. Istotne jest, że odstępstwa punktów od prostej mają charakter przypadkowy (losowy), a nie systematyczny.

Moglibyśmy teraz odczytać z wykresu doświadczalną wartość przyśpieszenia, bo, jak widać (równanie (1.45)), tangens kąta nachylenia naszej prostej do osi $\text{(}{t}^2\text{)}$, czyli współczynnik kierunkowy, jest równy liczbowo $\frac{a}{2}$. Jednakże zrobimy to nieco później, ponieważ prostą na il. 1.55 poprowadziliśmy trochę „na wyczucie” między punktami doświadczalnymi. Nie mamy pewności, czy nie można by jej dokładniej poprowadzić między tymi punktami. Bardziej precyzyjnie poprowadzimy prostą, jeżeli uwzględnimy niepewności pomiarowe.

Przeprowadzimy teraz dyskusję niepewności pomiarowych (należy najpierw zapoznać się z rozdziałem 1.D1. Dodatek: Ocena dokładności wyników pomiarów).

Liczbowym wynikiem naszego doświadczenia ma być przyspieszenie kulki. Wynik pomiaru jest wtedy pełny, gdy podajemy niepewność, z jaką go wyznaczono. Nasz końcowy wynik nie powstaje przez bezpośredni pomiar, lecz przez złożenie pomiarów bezpośrednich. Wobec tego jest on obarczony niepewnościami tych pomiarów. Zatem, podobnie jak to czyniliśmy w przypadku doświadczenia „Galileusz”, oceńmy najpierw niepewności pomiarów bezpośrednich.

a) Niepewności pomiarów bezpośrednich

Mamy dwie wielkości mierzone bezpośrednio – drogę $s$ i czas $t$. Przy ocenie niepewności pomiaru drogi $s$ należy wziąć pod uwagę to, że kreski, którymi zaznaczaliśmy odcinki drogi, mają pewną grubość (kreda) i że stosowaliśmy podziałkę centymetrową, która ma ograniczoną dokładność. Przyjmiemy więc, że maksymalna niepewność, z jaką mierzyliśmy drogę, wynosi:

Czas mierzyliśmy za pomocą stopera, którego dokładność jest wyznaczona przez wartość najmniejszej działki (w podanym przykładzie 0,1 s). Powinniśmy dodać jeszcze czas reakcji przy włączaniu i wyłączaniu stopera w przybliżeniu 0,1 s. Przyjmiemy więc, że maksymalna niepewność pomiaru czasu wynosi:

b) Niepewność pomiaru wielkości złożonej

Po przekształceniu wzoru (1.44) otrzymujemy:

więc przyspieszenie $a$, będące wynikiem końcowym pomiaru, ma postać ilorazu. Zatem możemy stosować taką samą regułę jak w przypadku doświadczenia „Galileusz”. Niepewność względna wyniku końcowego jest sumą niepewności względnych pomiarów bezpośrednich. Niepewności pomiarowe mogą powodować zarówno zawyżenie, jak i zaniżenie uzyskanego wyniku. Dlatego też, gdy zależy nam na uzyskaniu niepewności maksymalnej wyniku końcowego, przy jej ocenie uwzględnimy sytuację najbardziej niekorzystną, gdy niepewności wielkości mierzonych bezpośrednio „się sumują”, czyli dają ten sam skutek w postaci zaniżenia, bądź zawyżenia, wyniku. Dodajemy zatem do siebie niepewności względne:

Przez $\epsilon$ oznaczyliśmy względną niepewność przyspieszenia $a$. Tak więc niepewność $a$ wynosi:

Niepewność względną podwoiliśmy, ponieważ czas $t$ występuje we wzorze (1.46) na przyspieszenie w drugiej potędze $\text{(}{t}^2=t\cdot t\text{)}$.

Teraz możemy przystąpić do obliczeń szczegółowych. Obliczymy przyspieszenie dla każdego pomiaru, korzystając ze wzoru (1.46). Obliczymy też niepewność każdego wyniku, korzystając ze wzoru (1.48). W tym celu uzupełniamy tabelę z il. 1.54 o dodatkowe kolumny. W ostatniej kolumnie tabeli na il. 1.56 zamieszczone są wartości bezwzględne odchyleń każdego wyniku od średniej wartości przyspieszenia $a_{\text{śr}}=\mathrm{0,174}\text{m}/{\text{s}}^2$.

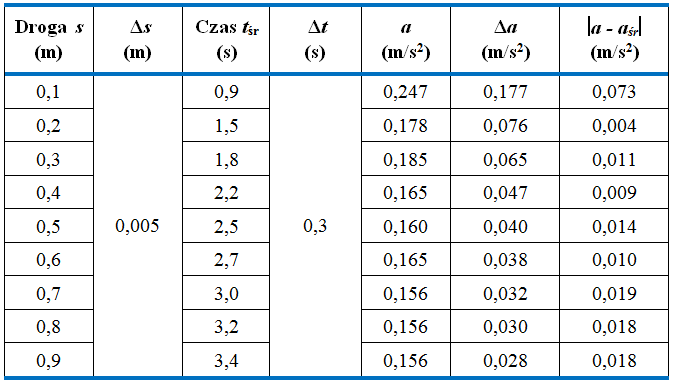
Zauważmy, że pierwszy wynik $a=\mathrm{0,247}\text{m}/{\text{s}}^2$ (uzyskany dla $s=\mathrm{0,1}\text{m}$ i $t=\mathrm{0,9}\text{s}$) istotnie odstaje od wszystkich pozostałych wyników. Jego odchylenie od średniej jest ponad czterokrotnie większe od odchyleń od średniej pozostałych wyników. Upoważnia to nas do stwierdzenia, że wynik ten jest obarczony istotnym błędem doświadczalnym (zwanym też błędem grubym lub po prostu pomyłką). Na dodatek widzimy, że jego niepewność jest pond dwukrotnie większa od niepewności pozostałych wyników. Te stwierdzenia powodują, że wynik ten eliminujemy z dalszej analizy.

Na il. 1.57 przedstawiono ostateczną postać tabeli wyników. Uzyskana w niej średnia wartość przyspieszenia wynosi $a_{\text{śr}}=\mathrm{0,165}\text{m}/{\text{s}}^2$.

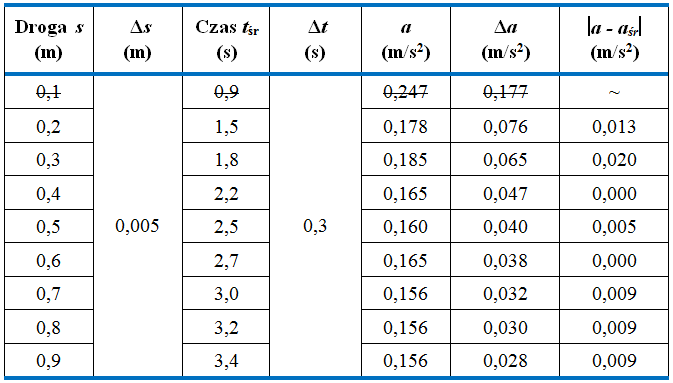
Teraz żaden pojedynczy wynik nie odstaje w sposób istotny od pozostałych. Możemy więc przyjąć, że uzyskana średnia wartość to wyznaczane przez nas przyspieszenie kulki. Jako niepewność tego wyniku przyjmiemy połowę różnicy między wynikiem największym i najmniejszym:

Ostatecznie więc wyznaczone przez nas przyspieszenie kulki wynosi:

Niepewności pomiarowe na wykresie $s\left(t^2\right)$

Uzupełnimy wykres na il. 1.55 o prostokąty niepewności pomiarowej. Stanowią one graficzne przedstawienie niepewności $\Delta s$ i $\Delta \left(t^2\right)$. Dzięki temu będziemy mogli dokładniej poprowadzić linię prostą na wykresie zależności $s$ od $t^2$.

Niepewność $\Delta s$ oceniliśmy jako równą $\pm \mathrm{0,5}\text{cm}$, natomiast niepewność kwadratu czasu $\Delta \left(t^2\right)$ musimy potraktować jako niepewność pomiaru złożonego, podobnie jak we wzorze (1.48):

$\frac{\Delta \left(t^2\right)}{t^2}=\frac{\Delta t}{t}+\frac{\Delta t}{t}=2\frac{\Delta t}{t}\Rightarrow \Delta \left(t^2\right)=2t\cdot \Delta t$

Dla każdego czasu $t$ obliczamy niepewność $\Delta \left(t^2\right)$. Obliczone wartości wpisujemy do tabelki (przykładowe dane w tabeli na il. 1.58).

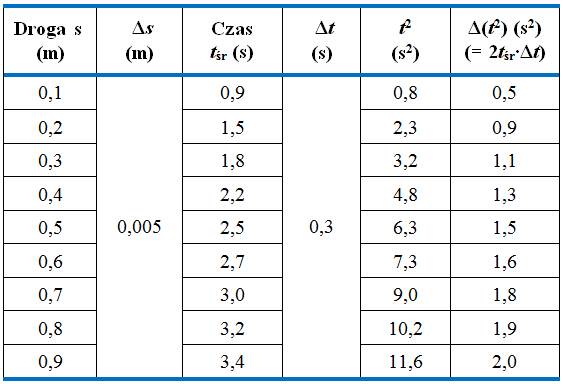
Każdy punkt doświadczalny na wykresie otoczymy tak zwanym prostokątem niepewności pomiarowych (il. 1.59) informującym nas o maksymalnej niepewności przy ustalaniu położenia punktu. Prostokąt niepewności ma podstawę równą $2\Delta \left(t^2\right)$, różną dla różnych punktów, i wysokość $2\Delta \left(s\right)=1\text{cm}$, jednakową dla wszystkich punktów.

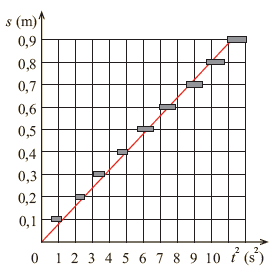
Teraz możemy śmiało poprowadzić prostą w pobliżu punktów doświadczalnych. Użyjmy linijki. Przystawmy ją do wykresu tak, by prosta przechodziła możliwe blisko wszystkich punktów. Nie popełnimy pomyłki, jeżeli prosta będzie przechodzić przez praktycznie wszystkie (powyżej 90%) prostokąty niepewności, jak na wykresie – il. 1.59. Zauważmy, że poprowadzona prosta ledwo „ociera się” o prostokąt pierwszego punktu $<s=\mathrm{0,1}\text{m};t^2=\mathrm{0,8}{\text{s}}^2>$. Fakt ten dodatkowo potwierdza słuszność naszej decyzji o wyeliminowaniu tego punktu z analizy.

Na koniec naszej analizy wyznaczymy graficznie przyspieszenie kulki $a$. Zgodnie ze wzorem (1.45) tangens kąta nachylenia prostej do osi $t^2$ (współczynnik kierunkowy prostej) jest liczbowo równy połowie przyspieszenia kulki:

Aby obliczyć wartość tangensa, możemy wziąć z wykresu rzędną i odciętą dowolnego punktu na prostej; najlepiej obrać punkt na końcu prostej. Weźmy zatem punkt o rzędnej równej 0,9 m. Wtedy odcięta wyniesie $\mathrm{11,4}{\text{s}}^2$ (patrz wykres na il. 1.55) i liczbowo:

Jest to liczba mianowana, zatem przyspieszenie kulki wyznaczone metodą graficzną wynosi $a_{\text{gr}}=\mathrm{0,158}\text{m}/{\text{s}}^2$. Wynik ten jest zgodny z uzyskaną wcześniej wartością $a=\mathrm{0,165}\pm \mathrm{0,015}\frac{\text{m}}{{\text{s}}^2}$, gdyż $a_{\text{gr}}\in <a-\Delta a;a+\Delta a>$:

Analizę wyniku tego doświadczenia można poszerzyć, korzystając z teorii ruchu bryły sztywnej (obracającej się kulki na równi pochyłej) – zob. rozdz. 4.9. Doświadczenie „Akceleracja BIS”.