2.4. Trzecia zasada dynamiki Newtona

Pierwsza i druga zasada dynamiki Newtona mówią nam o ruchu ciała, na które działa wypadkowa siła $\vec{F}=$ . Zasady te nie określają, skąd pochodzą siły działające na ciało. Newton zrozumiał, że aby na ciało zadziałała siła, potrzebne jest jakieś inne ciało. To inne ciało nie musi być w bezpośrednim kontakcie z ciałem, na które oddziałuje siłą. Zawsze jednak obowiązuje zasada:

Trzecia zasada dynamiki

Jeżeli ciało $A$ działa na ciało $B$ siłą $\vec{F}_{AB}$ , to ciało $B$ działa na ciało $A$ siłą $\vec{F}_{BA}$ , która ma tę samą wartość i ten sam kierunek, lecz przeciwny zwrot, czyli:

\vec{F}_{AB}=-\vec{F}_{BA}

Na il. 2.17 przedstawiono dwa ciała oddziałujące na siebie, jednak pokazane siły nie równoważą się, mimo że są zwrócone przeciwnie. Dzieje się tak, bowiem siły te są przyłożone do różnych ciał.

Ilustracja 2.17. **Ilustracja trzeciej zasady dynamiki Newtona**

Ilustracja 2.18. **Przeciąganie liny**

Oba zespoły działają na linę siłą o tej samej wartości, lecz przeciwnie zwróconą (póki lina pozostaje w spoczynku)

Ilustracja 2.19. **Siły przyciągania Ziemi i Księżyca**

Ziemia przyciąga Księżyc siłą $\vec{F}_{KZ}$ , również Księżyc przyciąga Ziemię siłą $\vec{F}_{ZK}$ . Te dwie siły są równe sobie – co do wartości, lecz przeciwnie zwrócone $\vec{F}_{KZ}=-\vec{F}_{ZK}$

Ilustracja 2.20. **Przykład działania trzeciej zasady dynamiki Newtona**

Zgodnie z trzecią zasadą dynamiki Newtona, silniki odrzucające spaliny działają na spaliny siłami takimi samymi (co do wartości) jak siły oddziaływania spalin na silniki, lecz przeciwnie zwróconymi $\vec{F}_{21}=-\vec{F}_{12}$

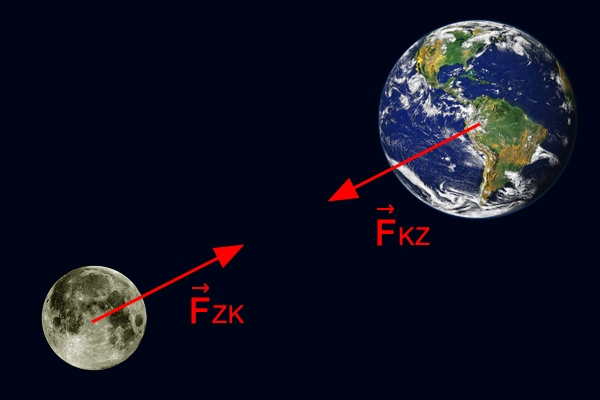
Trzecia zasada dynamiki stwierdza ponadto, że siły zawsze występują parami. Odrzutowiec działa siłą na odrzucane przez niego spaliny, natomiast spaliny działają na odrzutowiec taką samą siłą, ale w stronę przeciwną, dzięki temu uzyskuje on przyspieszenie i pokonuje opór powietrza. Ziemia przyciąga spadający kamień siłą $\vec{F}=m\vec{g}$ . Tymczasem kamień przyciąga Ziemię z siłą o takiej samej wartości. Dlaczego tego nie zauważamy? Ponieważ masa Ziemi $M$ jest znacznie większa od masy kamienia $m$ , więc przyspieszenie Ziemi $a$ , jest niezauważalnie małe. Zgodnie z zasadami dynamiki Newtona:

m\vec{g}=-M\vec{a}

skąd:

\vec{a}=-\frac{m}{M}\vec{g}

Ten przykład poucza nas dobitnie, że choć działające siły mają jednakowe wartości, to skutki działania tych sił są na ogół różne.

Przykład 3

Dwa klocki $A$ i $B$ o masach $m_{A}$ i $m_{B}$ połączone nicią leżą na idealnie gładkiej powierzchni poziomej (il. 2.21). Jaki warunek musi spełniać siła $\vec{F}$ przyłożona do klocka $B$ , aby nić się nie zerwała? Wiadomo, że nić wytrzymuje obciążenie równe $F_{max}$ .

Ilustracja 2.21. **Siły oddziaływania wzajemnego połączonych klocków**

Rozwiązanie: Siła zewnętrzna $F$ wywołuje przyspieszenie $a$ obu klocków. Na klocek $B$ działa siła $F$ i siła $F_{AB}$ , a na klocek $A$ działa tylko siła $F_{BA}$ . Zgodnie z drugą zasadą dynamiki Newtona, możemy napisać dwa równania, dla każdego klocka oddzielnie:

F-F_{AB}=m_{B}a

F_{BA}=m_{A}a

Zgodnie z trzecią zasadą dynamiki Newtona, wartości sił oddziaływania wzajemnego klocków są sobie równe, $F_{AB}=F_{BA}$ . Nić przenosi oddziaływania między klockami za pomocą siły naciągu $F_{N}$ , zatem $F_{AB}=F_{BA}=F_{N}$ . Mamy więc:

\begin{array}{c} F-F_{N}=m_{B}a\\ F_{N}=m_{A}a \end{array}\}

( 2.9 )

Dodając stronami te dwa równania, eliminujemy $F_{N}$ . Otrzymamy:

F=m_{A}a+m_{B}a=\left(m_{A}+m_{B}\right)a

Stąd przyspieszenie obliczymy ze wzoru:

a=\frac{F}{m_{A}+m_{B}}

Po podstawieniu tego wyrażenia do drugiego równania we wzorze (2.9), otrzymamy wartość siły naciągu nici:

F_{N}=m_{A}\frac{F}{m_{A}+m_{B}}

Nić nie ulegnie zerwaniu, gdy siła naciągu nici będzie mniejsza od siły $F_{max}$ , czyli gdy $F_{N} {mniejsze} F_{max}$ , zatem:

F_{N}=m_{A}\frac{F}{m_{A}+m_{B}} {mniejsze} F_{max}

skąd:

F {mniejsze} \frac{\left(m_{A}+m_{B}\right)F_{max}}{m_{A}}

Otrzymaliśmy zatem warunek na siłę $F$ , przy którym nić nie ulega zerwaniu.

Pytania i problemy

Sformułuj trzecią zasadę dynamiki Newtona i wyjaśnij jej zastosowanie na przykładzie.
Wykonując doświadczenie „Dyna”, stwierdziliśmy, że w stanie równowagi siła naciągu linki $N$ jest równa sile ciężkości odważnika $P_{1}$ (il. 2.14). Co trzeba zrobić, aby te dwie siły nie były równe sobie? Jak to można uzgodnić z trzecią zasadą dynamiki? Zastanów się, czy stan równowagi będzie trwał również wtedy, gdy ciężar odważnika $P_{1}$ i siła naciągu linki będą różne.
Stoisz na wadze i stwierdzasz, że Ziemia przyciąga cię siłą $P=65\, kG$ . Czy to znaczy, że i ty przyciągasz Ziemię siłą równą 650 N? Odpowiedź uzasadnij.
Scharakteryzuj wektory sił akcji i reakcji, o których mówi trzecia zasada dynamiki Newtona. Czy siły te mogą się równoważyć? Odpowiedź uzasadnij.
Wyjaśnij następujący „paradoks”: Chłopiec ciągnie sanki pewną siłą. W myśl trzeciej zasady dynamiki Newtona sanki ciągną chłopca w przeciwną stronę tą samą siłą. Dlaczego sanki w ogóle się poruszają?