4.1. Ruch postępowy i obrotowy bryły sztywnej
Aby opisać ruch ciała rozciągłego, musimy wziąć pod uwagę to, jak poruszają się jego punkty. Wyróżnimy dwa proste rodzaje ruchu – postępowy i obrotowy. W ruchu postępowym odcinek łączący dwa dowolne punkty bryły sztywnej przemieszcza się równolegle do siebie, zachowując stały kierunek w przestrzeni (il. 4.2a). W takim ruchu poszczególne punkty bryły mogą się poruszać po krzywych, a nawet po okręgach, niemniej ruch całości będzie postępowy, zgodnie z definicją tego ruchu. Łatwo można dojść do wniosku, że ruch tramwaju po torze prostym jest ruchem postępowym (il. 4.3a), natomiast ruch tego tramwaju na zakręcie nie jest ruchem postępowym (il. 4.3b). Wbrew pozorom ruch wagonika diabelskiego młyna jest ruchem postępowym (il. 4.3c), natomiast nie jest nim ruch wagonika karuzeli (il. 4.3d).

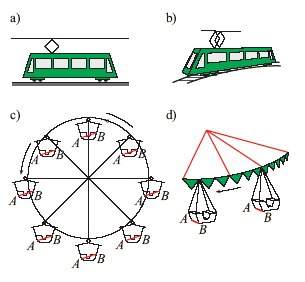
Ruch tramwaju na zakręcie, podobnie jak ruch wagonika karuzeli, jest ruchem obrotowym. Podczas ruchu obrotowego wszystkie punkty bryły zakreślają okręgi leżące na równoległych płaszczyznach, przy czym środki okręgów leżą na wspólnej prostej, zwanej osią obrotu (il. 4.2b). Różne punkty bryły, znajdujące się w różnych odległościach od osi obrotu, mają różne prędkości liniowe (il. 4.4), ale wszystkie punkty mają taką samą prędkość kątową .

Jeśli bryła jest w ruchu postępowym, to można ją zastąpić punktem materialnym, bo wszystkie jej części poruszają się z jednakową prędkością i zakreślają jednakowe tory. Całkowity pęd bryły da się przedstawić jako pęd punktu materialnego o masie , gdzie są masami poszczególnych elementów bryły. Pęd bryły jest równy sumie pędów elementów składowych, więc:
Dla porządku dodajmy, że wektor jest zaczepiony w punkcie zwanym środkiem masy bryły. Dokładny opis tego pojęcia zamieszczamy w 4.5. Środek ciężkości i środek masy.
Podobnie, energię kinetyczną bryły w ruchu postępowym można wyrazić tak jak energię kinetyczną punktu materialnego:
Natomiast w przypadku ruchu obrotowego, bryły nie można zastąpić punktem materialnym, ponieważ różne jej elementy mają różne prędkości liniowe. Możemy jednak wykorzystać fakt, że wszystkie elementy bryły mają jednakową prędkość kątową i opisywać jej ruch za pomocą wielkości dynamicznych zawierających tę prędkość. W tym celu posłużymy się pojęciami: moment pędu, moment bezwładności i moment siły.
Oczywiście, obliczenie energii potencjalnej bryły sztywnej w jednorodnym polu grawitacyjnym Ziemi sprowadza się do obliczenia energii potencjalnej punktu materialnego o masie położonego w środku masy bryły.
Pytania i problemy
- Wyjaśnij, dlaczego „bryła sztywna” jest ciałem modelowym, idealizacją realnych ciał. W jakim celu stosuje się taki model?
- Wytłumacz, czym się różni ruch obrotowy ciała od ruchu postępowego.
- Podaj trzy przykłady ruchu postępowego i obrotowego bryły sztywnej.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
