4.3. Twierdzenie Steinera. Zależność momentu bezwładności od położenia osi obrotu
Zgodnie ze wzorem (4.6) moment bezwładności zależy nie tylko od masy bryły, ale również od położenia osi, względem której go określamy. Istnieje zależność między momentem bezwładności układu względem dowolnej osi a momentem bezwładności względem równoległej do niej osi przechodzącej przez środek masy układu:
gdzie jest odległością między tymi osiami (il. 4.11). Zależność ta nosi nazwę twierdzenia Steinera.

Środek masy
Pojęcie to jest bardzo ważne i często stosowane w fizyce. Dlatego poświęcamy mu cały rozdział 4.5. Środek ciężkości i środek masy. Tutaj skrótowo podajemy najważniejsze dane potrzebne do zrozumienia treści rozdziału.
Pojęcie środka masy najłatwiej można wyjaśnić, rozważając bliskie mu pojęcie środka ciężkości (il. 4.12).

Pojęcie środka masy stosuje się nie tylko do dwóch ciał, ale również do układu wielu ciał i do brył sztywnych.
Wykażemy teraz słuszność twierdzenia Steinera dla układu dwóch punktów materialnych. W tym celu obliczymy ich momenty bezwładności względem dwóch równoległych osi, prostopadłych do płaszczyzny rysunku (il. 4.13), odległych od siebie o . Moment bezwładności względem osi przechodzącej przez środek masy wynosi:
Moment bezwładności możemy wyrazić wprost z definicji:
Z twierdzenia Pitagorasa: i . Po podstawieniu do wzoru (4.19) i po prostych przekształceniach otrzymamy:

Ponieważ i (zob. rozdział 4.5. Środek ciężkości i środek masy – definicja środka masy – oraz wzory (4.36) i (4.37)), więc (co mieliśmy wykazać).
Przykład 2
Znajdź wzór na moment bezwładności jednorodnego pręta względem osi prostopadłej do pręta przechodzącej przez jego środek masy (il. 4.14).

Przedstawiamy poniżej rozwiązanie, w którym nie korzystamy z wyniku Przykładu 1 z poprzedniego rozdziału. Zapoznaj się z tym rozwiązaniem i spróbuj samodzielnie znaleźć jednorodnego pręta względem osi prostopadłej do pręta i przechodzącej przez jego środek masy, ale z wykorzystaniem wyniku z Przykładu 1.
Rozwiązanie: Przyjmiemy, że wzór na moment bezwładności pręta (mającego masę i długość ) względem osi przechodzącej przez jego koniec ma postać:
gdzie jest bezwymiarowym współczynnikiem.
Zauważmy, że – moment bezwładności pręta względem osi przechodzącej przez środek masy – można przedstawić jako sumę momentów bezwładności jego połówek względem osi przechodzących przez ich końce. Zatem
Zgodnie z twierdzeniem Steinera:
Po przyrównaniu prawych stron równości (4.20) i (4.22) mamy . Stąd . Zatem, korzystając ze wzoru (4.21), otrzymujemy wzór wyrażający moment bezwładności pręta względem osi przechodzącej przez środek masy:
Przykład 3
Znajdź wzór na moment bezwładności jednorodnego walca względem osi przechodzącej przez jego środek (il. 4.15a).

Rozwiązanie: Zakładamy, podobnie jak w poprzednim przykładzie, że wzór na moment bezwładności (obecnie dla walca) ma postać:
Żeby znaleźć współczynnik , wytniemy z walca, w myśli, pierścień o wewnętrznym promieniu (il. 4.15b). Moment bezwładności będzie równy różnicy momentów dwóch walców o promieniach i oraz masach i (masa walca o ustalonej wysokości jest proporcjonalna do pola powierzchni kołowej podstawy ), zatem:
Skoro jest masą pierścienia, to:
Zatem, jeśli pierścień jest dostatecznie cienki (tzn. ), to:
Z drugiej strony, na podstawie wzoru (4.6) (patrz również Przykład 1),
Po porównaniu wzorów (4.24) i (4.25) i po uproszczeniu otrzymujemy:
Zatem dochodzimy do wniosku, że . Wzór na moment bezwładności dla walca przybiera postać:
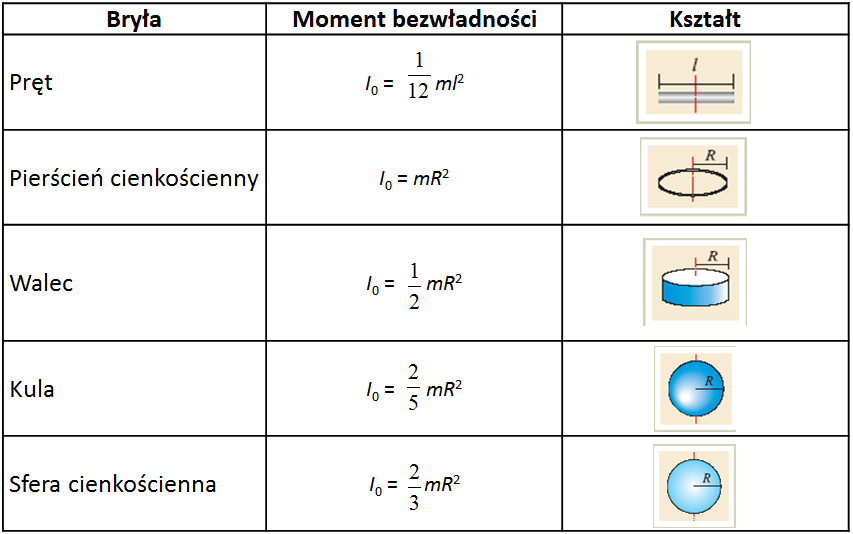
Wyprowadzenie wzorów dla innych prostych brył jednorodnych byłoby bardziej skomplikowane pod względem matematycznym, dlatego ograniczymy się tutaj do podania gotowych wzorów w tabeli (il. 4.16).
Przykład 4
Ile wynosi prędkość liniowa górnego końca słupa upadającego na ziemię? Słup początkowo znajdował się w pozycji pionowej i miał wysokość , następnie został podcięty u postawy.
Rozwiązanie: Energia potencjalna słupa o masie , w pozycji pionowej – środek masy słupa znajduje się na wysokości – wynosi:
Słup tuż przed upadkiem ma energię kinetyczną ruchu obrotowego (wzór (4.5)):
Moment bezwładności względem osi u podstawy słupa (patrz wzór (4.23) i twierdzenie Steinera (4.18)) wynosi:
Wykorzystując to wyrażenie, po przyrównaniu energii kinetycznej do energii potencjalnej słupa, otrzymamy:
Po uproszczeniu i uwzględnieniu, że prędkość liniowa górnego punktu słupa (tuż przed upadkiem) wynosi , otrzymujemy:
czyli:
Warto zwrócić uwagę, że prędkość ta jest większa, niż gdyby koniec słupa, rozumiany jako punkt materialny, spadał swobodnie pod wpływem własnego ciężaru. Zastanów się nad przyczyną tego faktu i spróbuj go objaśnić jakościowo.
Pytania i problemy
- W jakim celu stosuje się twierdzenie Steinera? Przytocz to twierdzenie.
- Znając moment bezwładności pierścienia cienkościennego o promieniu i masie względem osi przechodzącej przez jego środek (tabela na il. 4.16), oblicz moment bezwładności tego pierścienia względem osi przechodzącej przez jeden z punktów leżących na jego obwodzie.
- W wierzchołkach równobocznego trójkąta o boku
umieszczono małe kulki o jednakowych masach
. Oblicz moment bezwładności kulek względem osi równoległej do
wysokości trójkąta i przechodzącej przez kulkę.
Ilustracja 4.17. Układ kulek umieszczonych w wierzchołkach równobocznego trójkąta



 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
