4.9. Doświadczenie „Akceleracja BIS”
Wykonamy teraz doświadczenie, które jest pod wieloma względami podobne do doświadczenia „Akceleracja”, opisanego w rozdziale 1.13. Doświadczenie „Akceleracja”. Celem obecnego doświadczenia będzie zbadanie charakteru ruchu bryły sztywnej staczającej się z równi pochyłej. Będziemy chcieli wykazać, że jest to – podobnie jak w przypadku zsuwania się klocka z równi – ruch jednostajnie przyspieszony. Wyznaczymy też przyspieszenie staczającej się bryły i porównamy je z przyspieszeniem klocka zsuwającego się bez tarcia z identycznej równi.
Wykorzystamy przy tej okazji nabyte wcześniej umiejętności opracowania wyników pomiarów, w tym umiejętność przekształcania krzywej na wykresie w linię prostą (warto je sobie przypomnieć: rozdział 1.13. Doświadczenie „Akceleracja”). Graficzny sposób wyznaczania wartości parametru badanej zależności (tutaj parametrem jest przyspieszenie koła, występujące w zależności jego położenia od czasu) omówiliśmy wcześniej. Teraz przedstawimy graficzną metodę szacowania niepewności pomiarowej tak uzyskanego wyniku.
Doświadczenie wykonujemy w następujący sposób:
Z dwóch metalowych prętów połączonych odpowiednimi uchwytami (z kompletu elementów statywowych) budujemy „szyny”. Do szyn dołączamy linijkę wskazującą położenia lub na jednej z nich rysujemy kredą odpowiednie znaczniki położenia (il. 4.42). Zapewniamy też mocowanie szyn oraz możliwość podnoszenia jednej ich strony, by utworzyć równię pochyłą. Z tej równi staczać się będzie koło o średnicy kilkunastu centymetrów, osadzone na metalowej osi o średnicy 4 mm (il. 4.43). Oś ta opiera się na szynach. Tak mała średnica osi zapewnia, że koło osiąga niewielkie – w skali ludzkiej – prędkości liniowe, wygodne do obserwacji.


Koło puszczamy bez prędkości początkowej i za pomocą stopera mierzymy czas jego ruchu na coraz dłuższych odcinkach drogi. Mierzymy czas na drodze , na drodze itd. Koło puszczamy za każdym razem z tego samego punktu równi. Każdy pomiar powtarzamy trzykrotnie, aby łącznie otrzymać trzy serie pomiarów.
Jeśli w klasie kilkanaście osób dysponuje stoperami, to można każdą serię wykonać za jednym stoczeniem. Wszystkie osoby uruchamiają jednocześnie swoje stopery w chwili puszczenia koła; następnie każda osoba zatrzymuje swój stoper, gdy oś koła osiągnie zadane z góry, „przypisane do tej osoby” położenie . Stoper wskazuje wtedy czas , w którym oś koła minęła znacznik .
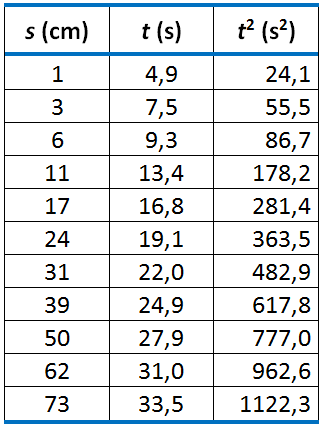
Wpisujemy wyniki pomiarów czasu do odpowiednich rubryk tabelki. Dla każdej wartości drogi obliczamy średni czas ruchu ciała i wpisujemy go do rubryki . Obliczamy wartości kwadratów czasów średnich i zapisujemy je w ostatniej rubryce tabelki. Na il. 4.44 przedstawiono przykładowe wyniki uzyskane w jednej ze szkół. W doświadczeniu tym równia została umocowana w taki sposób, że jej wysokość (dokładniej: różnica wysokości między punktami zamocowania) wynosiła 12 cm.
Wstępna analiza wyników pomiarów – wykresy
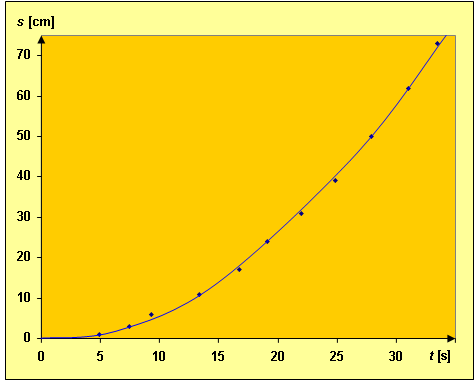
Sporządzamy wykresy zależności drogi od czasu dla wartości uzyskanych podczas pomiaru. Na osi rzędnych odkładamy drogę w centymetrach, a na osi odciętych – czas w sekundach. Pamiętajmy o doborze właściwej skali na osiach, aby wykresy były czytelne. Nanosimy punkty doświadczalne i wykreślamy krzywą, prowadząc ją między punktami doświadczalnymi (nie należy kreślić linii łamanej od punktu do punktu). Sprawdzamy, czy otrzymana krzywa przypomina parabolę. Teoretyczny wzór na drogę w ruchu jednostajnie przyspieszonym jest, jak wiemy, kwadratową funkcją czasu, czyli na wykresie przedstawia się jako parabola:
Jeżeli wykreślona krzywa na il. 4.45 przypomina parabolę, to znaczy, że ruch koła jest – zgodnie z oczekiwaniami – ruchem jednostajnie przyspieszonym. Jeżeli otrzymaliśmy taki wynik, możemy się cieszyć, jednakże możemy odczuwać pewien niedosyt, gdyż uzyskaliśmy tylko jakościowe potwierdzenie teorii.
Spróbujmy znaleźć potwierdzenie parabolicznego kształtu krzywej. Zastosujemy zatem procedurę „prostowania” paraboli opisaną w rozdziale 1.13. Doświadczenie „Akceleracja”. Jeżeli na osi rzędnych będziemy odkładać drogę , a na osi odciętych, zamiast wartości czasu , wartości kwadratów czasu , to powinniśmy otrzymać prostą. Wtedy w równaniu (4.63) jako zmienną niezależną traktujemy nie , ale , natomiast jako zmienną zależną. Otrzymujemy w ten sposób zależność liniową między a :
Wykres funkcji pokazany jest na il. 4.46.
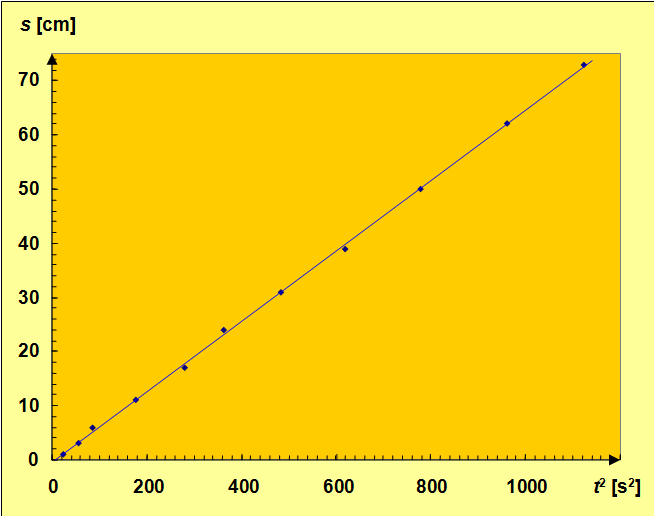
Wykreślona linia prosta przechodzi w pobliżu wszystkich punktów pomiarowych. Oceniamy, że rozrzut punktów wokół prostej jest losowy i spowodowany naturalną niepewnością pomiarową. Żaden z nich nie odstaje na tyle znacząco od prostej, by uznać odstępstwo za skutek poważnego błędu – pomyłki. Te właściwości funkcji potwierdzają, że linia na wykresie na il. 4.45 jest parabolą, a funkcja jest funkcją kwadratową. To z kolei świadczy o tym, że koło staczało się z równi ruchem jednostajnie przyspieszonym. W związku z tym możemy przystąpić do analizy niepewności pomiarowych i obliczenia przyspieszenia staczającego się koła.
Niepewności pomiarowe wielkości mierzonych bezpośrednio
Liczbowym wynikiem naszego doświadczenia ma być przyspieszenie koła. Wynik pomiaru jest wtedy pełny, gdy podajemy niepewność, z jaką go wyznaczono. Podobnie jak to czyniliśmy w przypadku poprzednich doświadczeń, oceńmy najpierw niepewności pomiarów bezpośrednich.
Mamy dwie wielkości mierzone bezpośrednio – drogę i czas . Przy ocenie niepewności pomiaru drogi należy wziąć pod uwagę to, że kreski, którymi zaznaczaliśmy odcinki drogi, mają pewną grubość (kreda), i że stosowaliśmy podziałkę centymetrową, która ma ograniczoną dokładność. Przyjmiemy więc, że maksymalna niepewność, z jaką mierzyliśmy drogę, wynosi:
Czas mierzyliśmy za pomocą stopera, którego dokładność jest wyznaczona przez wartość najmniejszej działki (w podanym przykładzie 0,1 s). Powinniśmy dodać jeszcze czas reakcji przy włączaniu i wyłączaniu stopera w przybliżeniu 0,1 s. Przyjmiemy więc, że maksymalna niepewność pomiaru czasu wynosi:
Z kolei maksymalna niepewność pomiarowa kwadratu czasu, traktowana jako niepewność iloczynu , dana jest wzorem:
Oznacza to, że prostokąty niepewności pomiarowej na il. 4.47 mają wszystkie jednakową wysokość równą , ale mają różne szerokości, każda równa .
Wykreślona linia prosta przechodzi przez wszystkie prostokąty niepewności pomiarowych. Utwierdza nas to w przekonaniu, że doświadczenie zostało przeprowadzone poprawnie, a wyciągnięte wnioski co do charakteru zależności są uprawnione – koło staczało się z równi ruchem jednostajnie przyspieszonym.
Graficzne wyznaczanie przyspieszenia i szacowanie jego niepewności pomiarowej
Mamy dwie możliwości wyznaczenia przyspieszenia i jego niepewności. Jedna, którą zastosowaliśmy w doświadczeniu „Akceleracja” (rozdz. 1.13. Doświadczenie „Akceleracja”), polega na obliczeniu przyspieszenia dla każdej pary pomiarów, obliczeniu średniej wartości tych wyników i ocenie niepewności na podstawie rozrzutu obliczonych wartości. Możesz tę procedurę powtórzyć; zacznij od odpowiedniego uzupełnienia tabelki na il. 4.44. Na koniec możesz porównać otrzymany wynik z wynikiem uzyskanym drugą metodą.
Druga metoda polega na obliczeniu nachylenia prostej optymalnej z wykresu na il. 4.47 i wyznaczeniu na tej podstawie przyspieszenia, zgodnie z procedurą opisaną w rozdziale 1.13. Doświadczenie „Akceleracja”. Kolejnym krokiem będzie poprowadzenie na wykresie tzw. prostych skrajnych. Na podstawie ich nachyleń uzyskamy oszacowanie niepewności pomiarowej przyspieszenia. Skoncentrujmy się na tej drugiej metodzie.
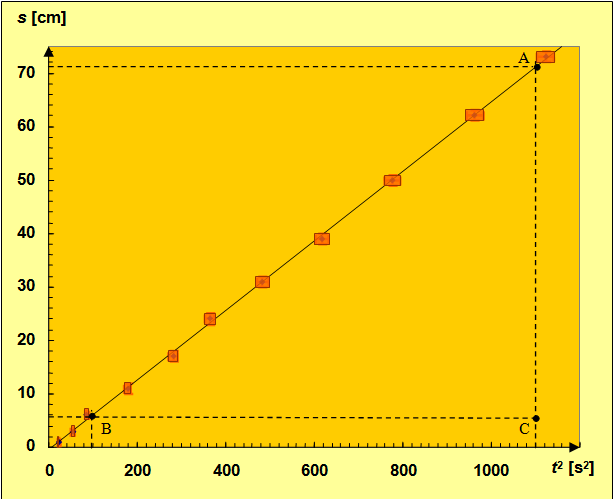
Punkty i na wykresie na il. 4.47 zaznaczono po to, by obliczyć nachylenie prostej optymalnej. Wybrano je dowolnie, choć precyzja wyniku jest tym lepsza, im leżą one dalej od siebie na tej prostej. Nachylenie obliczamy, podobnie jak tangens kąta między prostą a osią , dzieląc przez siebie długości dwóch przyprostokątnych i w trójkącie . Z wykresu odczytujemy współrzędne punktów i na tej podstawie obliczamy długości boków:
Szukane nachylenie jest ilorazem przez i wynosi . Nie dziwi nas, że jednostka nachylenia jest tożsama z jednostką przyspieszenia, gdyż zgodnie ze wzorem (4.64) nachylenie tej prostej jest równe połowie przyspieszenia koła. Wynika to z faktu, że wielkość jest współczynnikiem kierunkowym liniowej funkcji . Możemy więc stwierdzić, że koło staczało się z równi z przyspieszeniem:
By oszacować zakres niepewności pomiarowej nanosimy na wykres dwie proste „skrajne” (il. 4.48). Pierwsza, na której wybrano punkty i , ma możliwie małe nachylenie, zapewniające jednak jej przechodzenie przez wszystkie prostokąty niepewności. Z kolei druga ma możliwie duże nachylenie, ale także przechodzi przez wszystkie prostokąty; na tej wybrano punkty i . Dla zwiększenia czytelności wykresu nie nanosimy na nim prostej optymalnej, ale pozostawiamy prostokąty niepewności pomiarowej. Nie nanosimy też punktów i , których rolę objaśniliśmy na przykładzie punktu z il. 4.47.
Obliczymy, stosując takie samo postępowanie jak dla przyspieszenia , dwa skrajne nachylenia. Na tej podstawie obliczymy dwie skrajne wartości przyspieszenia: – najmniejsze dopuszczalne oraz – największe dopuszczalne.
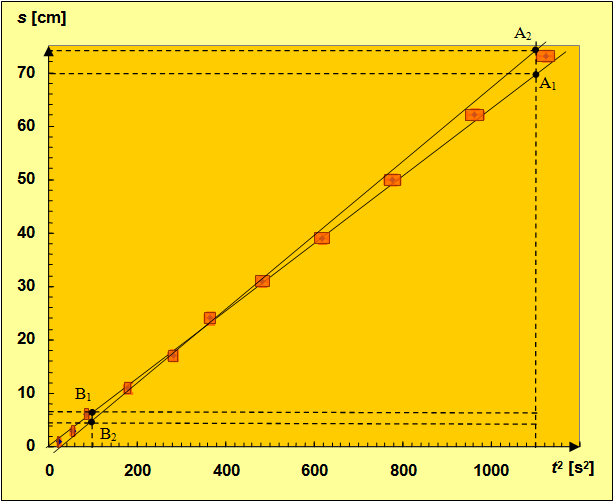
Do obliczenia odczytujemy z wykresu współrzędne punktów i :
Zatem:
Podobnie, do obliczenia odczytujemy z wykresu współrzędne punktów i :
Zatem:
Jako maksymalną niepewność pomiarową przyjmiemy połowę różnicy między i :
Ostatecznie więc przyspieszenie, z jakim koło stacza się z równi, wynosi:
Podsumowanie
Wszystkie postawione cele doświadczenia zostały osiągnięte. Zmierzone położenia staczającego się koła i czasy ich osiągania ułożyły się na wykresie w oczekiwany kształt – paraboli – co świadczy o jednostajnie przyspieszonym ruchu koła. Zostało to potwierdzone prostoliniowym ułożeniem się tych punktów na wykresie .
W doświadczeniu nie popełniono istotnych błędów (pomyłek), a odstępstwa punktów od optymalnej linii prostej na wykresie mieściły się w granicach niepewności pomiarowej.
Zastosowana graficzna metoda wyznaczenia przyspieszenia koła i oszacowania niepewności pomiarowej dała wynik:
Przyspieszenie to zostało wyznaczone ze względną niepewnością 4,6%, zadowalającą w warunkach szkolnych.
Uzyskane przyspieszenie jest zdecydowanie mniejsze od przyspieszenia , z jakim z takiej samej równi zsuwałby się bez tarcia klocek. Wysokość równi wynosiła 12 cm, zaś jej długość 100 cm. Kąt nachylenia użytej równi spełniał więc warunek:
a przyspieszenie wynosiłoby:
Przyspieszenie bryły staczającej się z równi jest zawsze mniejsze od przyspieszenia klocka, zsuwającego się bez tarcia. Można to uzasadnić zachowaniem energii. W przypadku klocka, cała energia potencjalna przekształca się w jego energię kinetyczną. W przypadku bryły, energia potencjalna przekształca się tylko częściowo w energię kinetyczną związaną z jej ruchem postępowym; reszta zostaje zamieniona w energię kinetyczną związaną z jej ruchem obrotowym. Dodatkowo, w naszym doświadczeniu, bryła nie toczy się na swoim obwodzie, lecz na osi o średnicy mniejszej od obwodu. Skutkiem tego jest zamiana znacznej części energii potencjalnej w energię kinetyczną obrotową, a bardzo niewielkiej części – w energię kinetyczną postępową. Wykonując doświadczenie mogliśmy zauważyć, że koło obracało się bardzo szybko, a przemieszczało się powoli.


 Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
Jeśli lubisz e-fizykę sprawdź nowe materiały projektu Stem4youth!
