Opis doświadczenia

Uwaga: W realnym doświadczeniu stosujemy rtęć, którą trudno jest zastąpić jakąś inną dostępną substancją, choć można próbować w jej miejsce użyć oleju. Ze względów BHP wymaga to szczególnej ostrożności, a w niektórych szkołach może być wręcz zakazane. Podobnie, w realnym doświadczeniu konieczne jest użycie dużej ilości bardzo gorącej (niemal wrzącej) wody, co też wymaga stosowania szczególnych środków ostrożności. Wobec tego proponujemy wykonać to doświadczenie wirtualnie – według załączonej animacji.

Potrzebna będzie rurka szklana o długości ok. 50 cm i średnicy ok. 6–8 mm zamknięta z jednego końca. Dobrze by było, gdyby rurka miała narysowaną skalę milimetrową. Do rurki wprowadzimy nieco rtęci w taki sposób, aby utworzył się koreczek rtęciowy o długości ok. 2 do 3 cm. Koreczek zamknie część powietrza w dolnej części rurki. Taka rurka nosi nazwę rurki Meldego.

Rurkę Meldego oraz termometr umieszczamy w statywie i oba przyrządy zanurzamy w wysokim pojemniku z wodą, który będziemy podgrzewać na kuchence elektrycznej (il. 6.14). Takie same przyrządy znajdują się w doświadczeniu wirtualnym. Nieco prostszym rozwiązaniem jest podgrzanie (doprowadzenie do wrzenia) sporej porcji wody w czajniku elektrycznym i napełnienie nią pojemnika. Wtedy wykonujemy pomiary w trakcie stygnięcia wody. Wadą tego rozwiązania jest długi czas oczekiwania na obniżenie temperatury użytej wody.

Naszym zadaniem jest doświadczalne sprawdzenie zależności objętości od temperatury danej za pomocą wzoru Gay-Lussaca (6.16):

W naszym doświadczeniu objętość powietrza $V$ jest iloczynem długości $l$ słupa powietrza pod koreczkiem rtęciowym i powierzchni $S$ poprzecznego przekroju szklanej rurki. Założymy, że $S$ jest wielkością stałą, więc po lewej stronie równania będziemy w liczniku mieli $lS$. Oznaczmy wartość stałej występującej po prawej stronie przez $a$ $\text{(}a=\text{const}\text{)}$ oraz przekształćmy wzór następująco:

Widzimy, że teoria procesu izobarycznego daje zależność proporcjonalną objętości (lub długości) od temperatury. Właśnie tę cechę procesu izobarycznego chcemy sprawdzić doświadczalnie.

Podstawowy warunek dla procesu izobarycznego, $p=\text{const}$, jest w naszym układzie doświadczalnym zachowany. Powietrze zamknięte w rurce znajduje się pod stałym ciśnieniem, gdyż w każdej temperaturze jest ono równoważone przez stałe ciśnienie hydrostatyczne rtęci (siła ciężkości skierowana w dół) oraz przez stałe ciśnienie powietrza znajdującego się na zewnątrz.

W doświadczeniu będziemy mierzyć temperaturę $t$ i długość $l$ części rurki z zamkniętym powietrzem. Długość $l$ jest miarą objętości $V$ gazu, zgodnie z zależnością:

Przyjęliśmy, że $S$ jest wielkością stałą, więc jeśli zależność $l\text{(}T\text{)}$ okaże się być proporcjonalna, to zależność $V\text{(}T\text{)}$ także będzie proporcjonalna. Postępowanie takie pozwoli nam uniknąć obliczenia $S$, co wprowadziłoby do naszego doświadczenia zbędną niepewność związaną z koniecznością pomiaru średnicy rurki $d$.

Pierwszy pomiar temperatury $t_1$ i długości $l_1$ wykonamy przy wyłączonym podgrzewaniu. Następne pomiary wykonamy przy włączonym podgrzewaniu kolejno co $10°\text{C}$.

Wyniki pomiarów wpisujemy do tabelki pomiarów (il. 6.15):

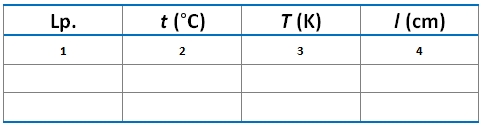
Kolumnę trzecią tabelki uzupełniamy, obliczając wartości temperatury w kelwinach według wzoru:

Wyniki pomiarów uzyskane w jednej ze szkół pokazano w tabeli na il. 6.16.

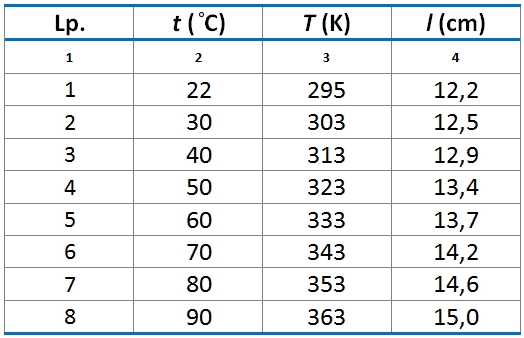
Przystępujemy do opracowania wyników doświadczenia.

Na podstawie danych z tabelki (rubryki 3 i 7) nanosimy punkty doświadczalne na wykres zależności $l$ od $T$.

Cieszymy się, jeżeli punkty doświadczalne układają się w pobliżu linii prostej. Oznacza to, że nasze doświadczenie potwierdza prawo Gay-Lussaca wyrażone za pomocą wzoru (6.16). Na il. 6.17 przedstawiono przykładowy wykres zgodny z danymi z tabeli na il. 6.16.

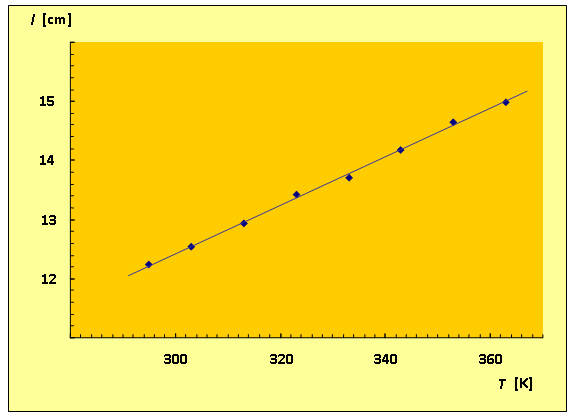
Oceniamy niepewności pomiarowe temperatury i długości i nanosimy je na wykres, tworząc prostokąty niepewności pomiarowych. W przykładowym doświadczeniu oceniono niepewność pomiaru temperatury jako $\Delta T=1\text{K}$; wynika to z najmniejszej podziałki na użytym termometrze. Niepewność pomiaru długości $\Delta l=1\text{mm}$, co także wynika z podziałki na rurce.

Po obliczeniu niepewności pomiarowych możemy uściślić przebieg naszej prostej optymalnej na wykresie tak, aby przechodziła możliwie blisko wszystkich punktów oraz by przecinała wszystkie prostokąty niepewności pomiarowej (il. 6.18). Gdyby nie udało się tak poprowadzić prostej optymalnej, to mogłoby znaczyć, że do naszych wyników wkradł się błąd doświadczalny. Mógłby on polegać, przykładowo, na tym, że koreczek był nieszczelny i w trakcie pomiarów z rurki powoli ulatywało powietrze.

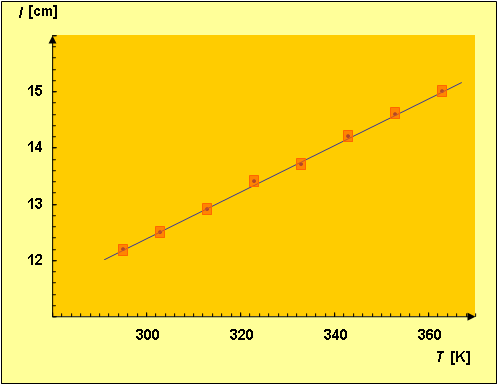
Uzyskane wyniki oraz wykres (il. 6.18) świadczą, że zależność $l\text{(}T\text{)}$ jest liniowa. Oznacza to, że zależność $V\text{(}t\text{)}$ jest także liniowa. By jednak w pełni potwierdzić zgodność wyników z prawem Gay-Lussaca, musimy wykazać, że uzyskana przez nas zależność $l\text{(}t\text{)}$ jest proporcjonalna, czyli że przechodzi ona przez początek układu współrzędnych.

Zwróćmy uwagę, że osie $T$ oraz $l$, il. 6.17 i il. 6.18, zostały wyskalowane w taki sposób, by przede wszystkim pokazać obszar temperatury, w którym przeprowadzono doświadczenie. Skutkiem tego, wykresy te nie pokazują obszaru w okolicach $T=0$ i nie pozwalają stwierdzić, czy uzyskana przez nas prosta optymalna przechodzi przez punkt $\text{(}T=0;l=0\text{)}$.

Rysujemy więc nowy wykres, na którym skalujemy oś $T$ od zera do 360 K zaś oś $l$ – od zera do 20 cm. Punkty pomiarowe zajmą wtedy stosunkowo niewielką część w prawym górnym rogu układu współrzędnych. Nanosimy prostą optymalną na tak przygotowany wykres i przedłużamy ją (linią przerywaną) do przecięcia z osią temperatury (il. 6.19a). Powinno ono trafić blisko punktu (0,0).